# O(n^3)
import itertools
def substring(s):
substrings = []
for i in range(len(s)):
for j in range(i + 1, len(s)+1):
substrings.append(s[i:j])
return substrings
# O(2^N)
def subset(s):
store = []
running = []
def helper(s, index, running, store):
if index == len(s):
store.append("".join(running))
return
running.append(s[index])
helper(s, index + 1, running, store)
running.pop()
helper(s, index + 1, running, store)
helper(s, 0, running, store)
return store
# O(N!)
def permutation(s):
#print(s)
if len(s) == 1:
return [s]
base = s[0]
array = permutation(s[1:])
newarray = []
for word in array:
for i in range(len(word)+1):
addedword = word[:i] + base + word[i:]
newarray.append(addedword)
#print(newarray)
return newarray
# O(N!)
def combination(s, r):
visited = set()
running, store = [], []
def helper(s, index, r, visited, running, store):
if len(running) == r:
store.append("".join(running))
return
if len(s) == index:
return
for i in range(index, len(s)):
if i not in visited:
running.append(s[i])
visited.add(i)
helper(s, index + 1, r, visited, running, store)
running.pop()
visited.discard(i)
helper(s, 0, r, visited, running, store)
return store
s = "abc"
#s = "stackover"
print(substring(s))
print(subset(s))
print(combination(s, 3))
print(combination(s, 2))
print(combination(s, 1))
print(permutation(s))
print("PYHTON itertools library ")
import itertools
import math
print("PERMUTATION For array :3P3")
print(math.factorial(3))
print(list(itertools.permutations([1,2,3])))
print("PERMUTATION [1,2,3], 2 :3P2")
print(math.factorial(3)//math.factorial(3-2))
print(list(itertools.permutations([1,2,3],2)))
print("PERMUTATION [1,2,3], 1 : 3P1")
print(math.factorial(3)//math.factorial(3-1))
print(list(itertools.permutations([1,2,3],1)))
print("COMBINATION [1,2,3], 3 : 3C3")
print(math.factorial(3)//(math.factorial(3-3)*math.factorial(3)))
print(list(itertools.combinations([1,2,3], 3)))
print("COMBINATION [1,2,3], 2 : 3C2")
print(math.factorial(3)//(math.factorial(3-2)*math.factorial(2)))
print(list(itertools.combinations([1,2,3],2)))
print("COMBINATION [1,2,3], 1 : 3C1")
print(math.factorial(3)//(math.factorial(3-1)*math.factorial(1)))
print(list(itertools.combinations([1,2,3],1)))
def nPr(n, r):
return int(math.factorial(n)//math.factorial(n-r))
def nCr(n, r):
return int(math.factorial(n)/(math.factorial(n-r)*math.factorial(r)))
Monthly Archives: October 2021
Topological Sort
Topological sorting for a graph is not possible if the graph is not a DAG.
from collections import defaultdict
class Graph:
def __init__(self, vertices):
self.graph = defaultdict(list)
self.vertices = vertices
def addEdge(self, u, v):
self.graph[u].append(v)
def getDegree(graph, vertices):
degrees = [0]*vertices
for v in graph:
for vv in graph[v]:
degrees[vv] += 1
return degreesBFS TopologicalSort
def topologicalSort(graph) :
indegrees = getDegree(graph.graph, graph.vertices)
visited = set()
path = []
for v in range(graph.vertices):
#print(v)
if indegrees[v] == 0:
bfs_ts(graph.graph, v, visited, path)
return path
import collections
def bfs_ts(graph, v, visited, path):
queue = collections.deque()
queue.append(v)
visited.add(v)
while queue:
v = queue.popleft()
path.append(v)
for nei in graph[v]:
if nei not in visited:
visited.add(nei)
queue.append(nei)
# If vertices left, indegree ==0 will add the pathDFS TopologicalSort
def topologicalSort(graph):
degree = getDegree(graph.graph, graph.vertices)
visited = set()
path = []
for v in range(graph.vertices):
if degree[v] == 0:
dfs_ts(graph.graph, v, visited, path)
return path[::-1]
def dfs_ts(graph, v, visited, path):
visited.add(v)
for nb in graph[v]:
if nb not in visited:
dfs_ts(graph, nb, visited, path)
path.append(v)Test topologicalSort
myGraph = Graph(5)
myGraph.addEdge(0, 1)
myGraph.addEdge(0, 3)
myGraph.addEdge(1, 2)
myGraph.addEdge(2, 3)
myGraph.addEdge(2, 4)
myGraph.addEdge(3, 4)
print(topologicalSort(myGraph)) # [0, 1, 2, 3, 4]
myGraph = Graph(6)
myGraph.addEdge(5, 2)
myGraph.addEdge(5, 0)
myGraph.addEdge(4, 0)
myGraph.addEdge(4, 1)
myGraph.addEdge(2, 3)
myGraph.addEdge(3, 1)
print(topologicalSort(myGraph)) # [5, 4, 2, 3, 1, 0]"Choosing A Database
Key-Value Database
Used for storing key-value pairs in a distributed manner.
Amazon DynamoDB (DAX caching for DynamoDB), Redis(Redis provides a different range of persistence options), Aerospike
Common Uses:
some of the most common use cases of key-value databases are to record sessions in applications that require logins.
a shopping cart where e-commerce websites can record data pertaining to individual shopping sessions.
storing clickingstream data
Web Cache for Radis and Aerospike
Pros:
Simplicity, Speed, Scalability
Cons:
Simplicity, No query Language
Document database
Used to storing JSON documents
MongoDB, CouchDB, CosmosDB
Common Uses:
User profile
Book Database
content management (Catalogs)
Patient Data
Pros: Schemaless
Cons: Consistency, Atomicity
it would be possible to search for books from a non-existent author.
a change involving two collections will require you to run two separate queries (per collection).
Graph Database
A graph is composed of two elements: a node and a relationship. Emphasized connections between data elements, storing related “nodes” in graphs to accelerate querying
Amazon Neptune, Neo4j, Tiger DB
common Uses:
Real-time recommendation engines
Fraud Detection
Identity and access management (IAM)
Ledger Database
A ledger database is log-centric. Store using an append only record journal. Here, the term “log” means a storage abstraction that is “an append-only, totally-ordered sequence of records ordered by time”.
Amazon QLDB
Common Uses:
Store financial transactions
Maintain claims history
Centralize digital records
Distributed Data processing System
Apache Hadoop, Spark
DBMS (Relational Database-SQL)
With ACID for consistency with fixed schema
mysql, postgresql, Oracle
Common Uses (write and update heavy):
Relational databases are better to use with payment transaction records
Columnar Database (DBMS)
A columnar database stores data in columns rather than the rows used by traditional databases. Columnar databases are designed to read data more efficiently and return queries with greater speed. it store data across tables that can have very large number of columns. If data has large amount of scale such as Google Search “Pyhton”:[23, 45, 67, 89, 123, 234,789,2344,3345,5543,6545,7545,7955,8099,12344,14566,14767,14890,14891,14892,… ]. This is a good candidate for columnar database. It works well with Scatter and Gather strategy for faster throghput.
Cassandra (noSQl, Columar), Apache HBase, Amazon Redshift, PostgreSQL, MariaDB
Common Uses (read heavy):
internet search
other large-scale web applications
Pros:
A columnar database is preferred for analytical applications because it allows for fast retrieval of columns of data. Columnar databases are designed for data warehousing and big data processing because they scale using distributed clusters of low-cost hardware to increase throughput.
Queries that involve only a few columns.
Cons:
Incremental data loading
Queries against only a few rows
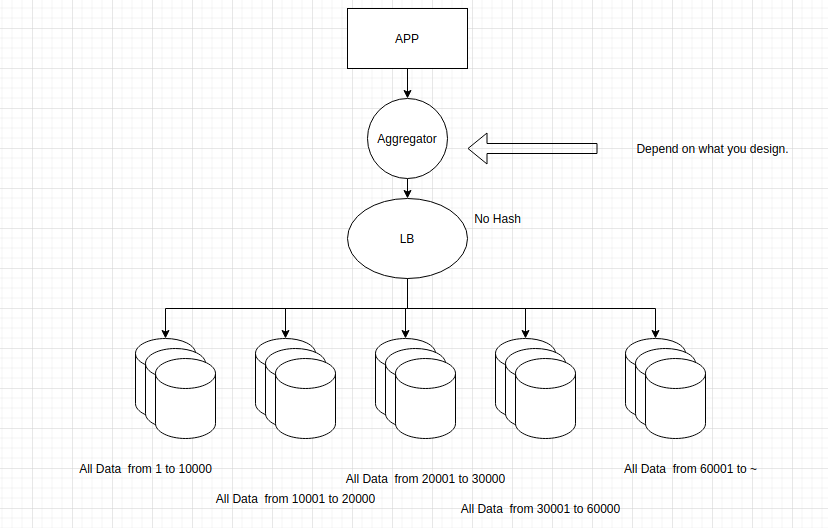
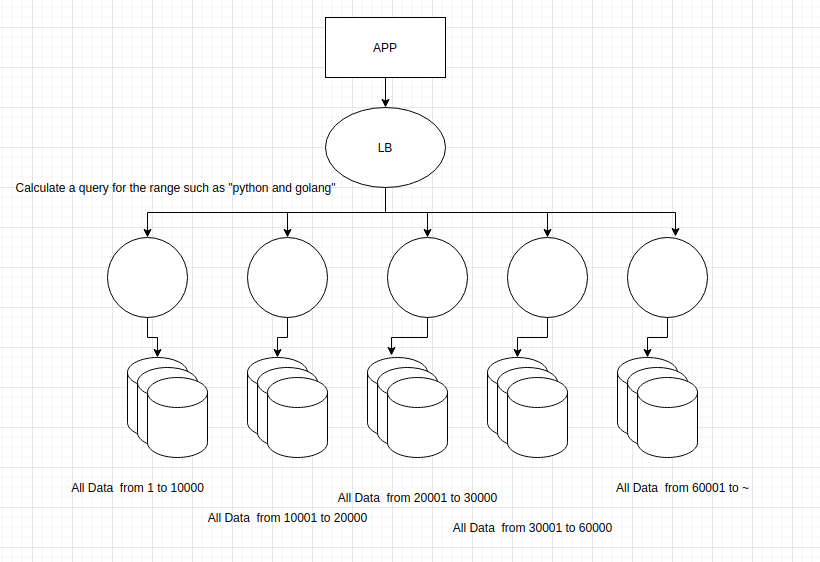
How to Choose
- Will you be doing more reading or writing? Relational systems are superior if you are doing more writing, as they avoid duplications during updates.
- How important is synchronisation? Due to their ACID framework, relational systems do this better.
- How much will your database schema need to transform in the future? Document databases are a winning choice if you work with diverse data at scale and require minimal maintenance.
